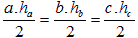Триъгълник. Ъгли на триъгълник

О – Геометрична фигура, която се състои от три точки, нележащи на една права, и съединяващите ги три отсечки.

Видове триъгълници според страните:

Определения

Разностранен – Триъгълник с различни страни.
Равнобедрен – Триъгълник с две равни страни. Равните страни се наричат бедра, а третата страна се нарича основа.
Равностранен – Триъгълник с три равни страни.

Видове триъгълници според ъглите:

Височини на триъгълник:

Определение – Отсечка, която е перпендикулярна на страна и минава през срещулежащия връх.
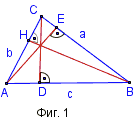
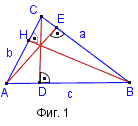
Височини при остроъгълен триъгълник – На Фиг. 1 това са: AE = h_a, BH = h_b, CD = h_c.

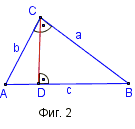
Височини при правоъгълен триъгълник – На Фиг. 2 това са: AC = b = h_a, BC = a = h_b, CD = h_c.

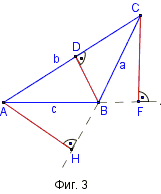
Височини при тъпоъгълен триъгълник – На Фиг. 3 това са: AH = h_a, BD = h_b, CF = h_c.

Медиани на триъгълник:

О – Отсечката, която съединява връх със средата на срещуположната му страна.

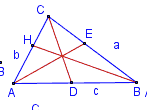
На фигурата това са: AE = m_a, BH = m_b, CD = m_c.

Ъглополувящи на триъгълник:

О – Отсечката, която дели съответният ъгъл на две равни части.

На фигурата това са: AE = l_a, BH = l_b, CD = l_c.

Параметър и лице на триъгълник:

Лице S на произволен ΔABC (Фиг. 1):
(1): S _ΔABC =

Лице S на правоъгълен ΔABC с катети a и b
(2): S _ΔABC =

Вътрешни ъгли

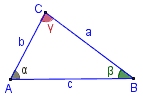
T за произволен триъгълник – Сборът от ъглите на всеки триъгълник е равен на 180°, т.е.
α + β + γ = 180° (виж чертежа).
T за правоъгълен триъгълник – Сборът от острите ъгли на правоъгълен триъгълник е равен на 90°, т.е.
α + β = 90° (при положение, че γ = 90°).

Външни ъгли

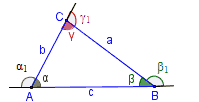
Определение – ъгъл, който е съседен на вътрешен ъгъл на триъгълника. На фигурата, това са ъглите α₁, β₁ и γ₁.
Теорема – Всеки външен ъгъл е равен на сбора на два вътрешни, несъседни нему ъгли. От фигурата следва, че
α₁ = β + γ.
β₁ = α + γ.
γ₁ = α + β.
Следствие – Всеки външен ъгъл на триъгълник е по-голям от всеки несъседен с него вътрешен ъгъл, т.е.
α₁ > β, α₁ > γ.